Continuing from Chapter 4: The Language of the Mind
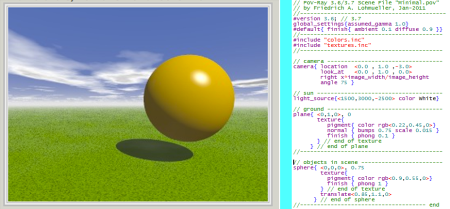
The computational function performed by mental imagery can be better understood by comparison with computer ray-tracing applications that perform a very similar computational function. Figure 1 shows an example of a ray-traced image of a scene from Friedrich A. Lohmueller’s most excellent web site generated by the free open-source ray-tracing program POV-Ray, consisting of a sphere floating in space above a ground plane, under the dome of a synthetic sky. A light source is modeled in the sky, whose rays illuminate the sunny side of the sphere, which casts a shadow on the ground plane below. This is exactly the kind of image that might be evoked in mental imagery by the words “Imagine a sphere floating in the air”. Any artist worth their salt could compose such a picture on demand using paint and canvas to record a mental image that corresponds to those words. The image itself is two-dimensional, a mere projection of the mental image that it depicts. But it requires consideration of the full three-dimensional spatial configuration to correctly compute the scene, especially the patterns of light and shadow on the sphere, as well as the shadow it casts on the ground below.
The computational algorithm used in ray-tracing involves tracing every ray in straight lines radiating outward from the light source, and following its path through empty space until it strikes the surface of an object in the scene. If the surface is opaque, with a certain color, then the modeled ray is absorbed and re-emitted in that color in all directions from every point on the illuminated surface, as if the whole illuminated surface were glowing with that color. If the object is shiny, then a portion of the ray is traced through a specular reflection as in a reflection through a mirror, creating a shiny highlight, and if the object is transparent, the ray-tracing algorithm traces the ray through the transparent object, modeling the proper refraction and partial absorption, or filtering, of the transparent, possibly colored medium. Every single ray radiating from every light source is traced in this manner through any number of reflections, refractions, and re-emissions through the scene. Any rays that happen to stray in the direction of the viewpoint or ‘camera’ position, if they fall within the frame of the rendered image, leave a trace on the image where the accumulated rays paint out the ray-traced image of the imagined scene. This is an extraordinarily computation-intensive process that takes many billions of computer cycles to compute. (Actual ray-tracing applications reduce the computational load considerably by starting at the final image plane and tracing the light rays backward toward the sources, thus only having to compute those rays that end on the output image)
The remarkable thing is that the human mind can perform this kind of computation virtually instantaneously, in a flash of mental imagery, strongly implicating a parallel analog computational strategy that solves the problem by spatial analogy. Although it takes an artist a certain amount of training and practice to learn to paint realistic scenes with the proper shading, shadows, and reflections, even young children can immediately interpret the result, even with a scene as complex as that in Figure 2, (“Balcony” from the POV-Ray gallery) with multiple cast shadows, reflections, refractions, and complex geometrical shapes. The compelling appeal of ray-tracing algorithms is not so much that computers are capable of performing the computations, which is amazing enough in itself, the real amazing thing is that people can correctly interpret the results, and they do so, even young children, instantaneously and effortlessly, without even any awareness that they are doing a computation at all.
The ray-tracing algorithm demonstrates explicitly the computational function served by the faculty of mental imagery, although what can take many hours of crunching in a digital computer seems to occur near-instantaneously in the human mind.
Ray-tracing applications use a geometrical code to define the structures to be rendered. For example the sphere at the center of the scene in Figure 1 is defined by a POV-Ray function sphere{ } which is given parameters that define its location scale, orientation, and the color of its surface. The ground plane is defined with the function plane{ }, which is also assigned a location and orientation and color, or patterns of color. These functions serve the same purpose as the concept node in visual perception, representing the general concept in abstract invariant terms, while providing for parameters that can specify any particular cube or plane while conforming to the invariant formula. Friedrich A. Lohmueller’s excellent POV-Ray tutorial demonstrates the great variety of different shapes that can be defined by simple geometrical functions, illustrated here, from spheres and cylinders and cones, through boxes and prisms.
Shapes and surfaces can also be defined by any mathematical function that specifies a location for every point in the surface, for example using paraboloids and hyperboloids, as shown here, polynomial, exponential, sinusoidal, parametric, any mathematical function that defines a surface or volume. 
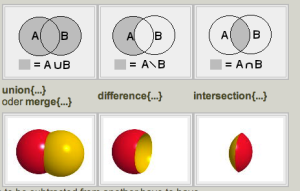
Compound shapes can be built up by Constructive Solid Geometry (CSG) operations, logical set-theoretic operations between volumetric solids, such as unions, intersections, difference, etc. For example the union of the red and yellow spheres defines a shifted double-sphere. The yellow sphere subtracted from the red sphere cuts a
spherical bite, or void from the red sphere, while the intersection of the two spheres is the volume of their geometrical intersection, a lens-shaped volume that perfectly models a spherical lens.
Shapes can also be defined by extrusion, by translating a three-dimensional shape along a three-dimensional path through space, thereby sweeping a volume through that space as shown in these examples. For example the torus (shown above) is defined by sweeping a flat circle around a circular path normal to its surface. The shape, size, and orientation, and even color of the moving shape can change as a function of position along the path, resulting in shapes that swell and shrink in characteristic ways.
Compound shapes, or arrays of shapes can be constructed by repeating copies of a basic shape, each one translated, rotated, scaled, or otherwise reshaped to create ever more complex compound shapes.
You can define smoother blob objects using some kind of distance metric from some reference frame, which you can imagine as a kind of haze whose density varies with distance from the frame. A density threshold defined in that haze will in turn define a surface that encompasses a volume. For example the pink triangular blob shown in the upper-left is defined on a triangular frame between three vertex points, with a larger distance metric around the points, and a smaller metric around each triangular side. The two metrics are blended with a nonlinear equation, resulting in a smooth blobby shape that necks continuously from spherical to cylindrical form.
The surfaces of objects can be painted with patterns of ‘pigment’, colors and textures, which are defined in the very same language, i.e. Euclidean geometry, as the language of three-dimensional shape.
If you modulate regular patterns with some kind of randomized turbulence, you can generate a great variety of different patterns that bear striking resemblance to a great variety of natural phenomena.
Randomized functions and fractals generate more realistic random patterns.
The shapes themselves can also be modulated or replicated in regular arrays, to define compound objects composed of a multitude of sub-units. Random or fractal functions can make these structures quasi-periodic, more similar to certain natural phenomena.
POV-Ray is a truly magnificent tool for defining three-dimensional scenes from your imagination. Its dimensions are those of the artist, color, space, form, and light, the dimensions of conscious experience. But its genius is in the fact that, like virtually all other ray-tracing apps, it uses the natural language of visual perception to express its geometrical structure, because that is the code we all understand. It is the way we think about shapes, that is the way we break down compound shapes into their geometrical primitives. We use this visual code not only in free-wheeling visual imagination, but also in perception. Visual perception is the act of hallucinating a scene that is consistent with all the sensory evidence. Perception is as much an act of creation, as it is an act of detection. If an artist were given any of the two-dimensional ray-traced scenes above, and commissioned to construct a three-dimensional painted sculpture of the scene, the computational function that he is comissioned to perform is exactly the computational function of perception: The input is a two-dimensional image not unlike a retinal image: The output is the rich three-dimensional experience that you have, immediately and unconsciously, as soon as you just glance at any of the ray-traced images above.
There is a general principle encapsulated in this mathematical approach to defining geometrical shapes, and it is a foundational principle that underlies all of mathematical thought. Every mathematical function, whether a simple linear or planar function, a circular or cylindrical or spherical arc or shell, or something more complex like a polynomial, exponential or logarithmic, or sinusoidal function in one, two, or three dimensions. It is that whatever the formula that defines the shape, that shape is defined to infinite precision. The function defines a pattern that is independent of scale. It is a pure and perfect descriptor of shape to essentially infinite resolution. The appearance of this concept in ray-tracing software reflects the deep intuitive basis of this way of representing shape in the human mind. Ray-tracing software is designed by people to be used by people, and that is why it uses basic geometrical concepts starting with points, lines, and planes, to define the shapes that create the imaginary scenes. This is the way that we think about shape, whether in perception or in mental imagery and imagination.The reason why ray-tracing algorithms employ the primitives of euclidean geometry is the same reason why Euclid chose those same primitives in the first place, because that is the way we conceptualize shape. Euclidean geometry was not an invention, but more of a discovery of the basic elements of geometrical thought, and successive generations of geometry students accept euclidean geometry not as dogma, but because they find it consistent with their natural intuitions about shape, a product of the long evolution of our perceptual and conceptual systems.
Continued Chapter 6: Let There Be Light!
slehar 