The Inverse-Optics Problem

Continuing from Chapter 6: Let There Be Light!

Visual perception is a constructive, or generative function that interprets the visual stimulus by constructing a three-dimensional model of the configuration of objects and surfaces in the external world that is most likely to have been the cause of the given stimulus. We can observe this constructive function in visual illusions like the Kaniza figure, Tse’s spiral worm, Idesawa’s spiky sphere, and Tse’s Loch Ness Monster. Each of these illusions are perceived as three-dimensional objects and surfaces, with a distinct experience of depth and surface orientation at every point on every visible surface. In other words, the experience itself is a three-dimensional structure, a model of external reality expressed in an explicit spatial code, a volumetric image projection mechanism.

Visual perception is analogical in nature: We perceive objects by constructing spatial analogies of them and experiencing those analogies, which we come to believe to be the objects themselves, perceived out where they lie beyond the sensory surface. Visual perception will always seem profoundly paradoxical until we see through the Grand Illusion and recognize the world of experience for what it is: A miniature virtual-reality replica of the external world in an internal representation.

The primary function of visual perception is the construction of this volumetric spatial interpretation of objects and surfaces in the world that are most likely to have been responsible for the visual stimulus. This is known as the inverse-optics problem, i.e. to undo the optical projection from the three-dimensional world to the two-dimensional retinal projection. This problem is mathematically under-constrained, because there is an infinite range of three-dimensional spatial interpretations that correspond to any given visual stimulus. For example a rectangle on the retina could correspond to any of the infinite range of irregular quadrilaterals spanning different depths, whose corners correspond to those of the retinal image. How does the visual system select from this infinite set the one that we perceive?

I propose that the only feasible way to solve such a computationally intractable problem is by way of a parallel analog wave-like algorithm that essentially constructs, or reifies, every possible interpretation simultaneously and in parallel, before selecting from that infinite set the one (or more) most stable interpretation. And the selection criterion seems to involve Gestalt principles of simplicity and symmetry. This is where mathematics enters perception.

Hochberg & Brooks(1960) found that the probability that a line-drawing is interpreted as 2-D as opposed to 3-D depends on the simplicity of the interpretation in 2-D compared to 3-D. For example figure A below is perceived as a cube with equal sides and all right angles, whereas as a 2-D pattern  there are 7 tiles with different angles and side lengths. Figure D on the other hand makes a simple pattern in 2-D, and thus is perceived easily as a 2-D figure with six identical equilateral triangles, whereas in 3-D it represents an unlikely singular viewpoint along a diagonal axis, which is evidently more difficult to perceive.

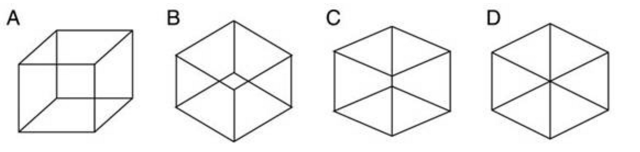
The fact that most of these figures can be perceived as 2-D or 3-D, with a particular preference for one over the other, and the fact that the ambiguous cases can be observed to flip bistably between two states, suggests that the visual system has constructed both alternatives, and is weighing them against each other in real-time to see which is the simpler interpretation.

Indeed this is the same principle in evidence in the illusions introduced earlier. A triangle occluding three perfect circles in the Kanizsa figure trumps an interpretation as three pac-man features perfectly aligned.  Peter Tse’s volumetric worm tends to be perceived with a simple cylindrical body, ends capped with perfect hemispheres, bent into a regular spiral around a regular white cylinder. Likewise with Idesawa’s spiky sphere, and Tse’s sea monster. This is a visual system that is based on symmetry, the perceptual equivalent of Occam’s Razor: In the absence of evidence to the contrary, the most likely interpretation is the most symmetrical one. Not because everything in the world is symmetrical. Far from it! But because symmetry is the primitive operational principle of the visual system: we perceive shapes by their symmetries and by their their violations of symmetry.

The metric found by Hochberg & Brooks to correspond with the perceptual preference for a 2-D or 3-D interpretation involved the number of edges of the same length, and the regularity of the angles between edges. This corresponds to the Gestalt principle of prägnanz, or simplicity, the simplest interpretation is the most stable in perception. This also corresponds to a metric involving resonance in a 2-D and 3-D context.

Start with A, inverse-project into depth, but also within xy plane

Mark centers of symmetry

Extrapolate to implications

Competition between different depths

various examples

Next chapter: Visual ornament

 

 

 

 

Consider Peter Tse’s volumetric worm depicted below in figure A. The computational function of perception can be defined as the expansion of that 2-D stimulus into a full 3-D experience as shown below in figure B.

 

 

 

 

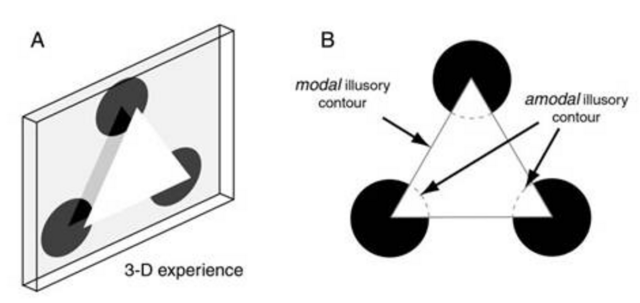
The Kanizsa figure is actually a three-dimensional perceptual experience as the foreground triangle is perceived to occlude three complete circles that complete behind it. There are two aspects to this illusion: There is the amodal contours of the hidden sectors of the three circles that are perceived “invisibly” behind the triangle, and then there are the modal contours of the triangle that take on an actual brightness difference across the illusory edge.

 

 

 

 

 

 

 

The significance of symmetry is apparent in the phenomenon of the kaleidescope, whose symmetrical patterns are instantly perceived before we have time to think about it. When you think of the computational algorithm required to detect this kind of symmetry it is a combinatorial nightmare, as every piece of the image must be matched against every other piece at every different orientation.  The phenomenon of the kaleidescope strongly implicates a parallel analog wave-like computational principle whereby global patterns of symmetry emerge spontaneously from the simultaneous action of innumerable local forces. This is the Gestalt principle of emergence.

The emergent symmetry-detection system must operate in a full 3-D context because the simplicity of the 3-D perceptual interpretations is not at all apparent in 2-D projection.

 

 

 

 

 

The way that the visual system addresses this vast expansion of possibilities is to construct, or reify, every possible interpretation of the stimulus simultaneously and in parallel.

We can see this simultaneous parallel competition between equally likely interpretations in carefully contrived visual illusions that give exactly equal weight to alternative interpretations, resulting in a bistable, or multi-stable percept that alternates randomly between alternative interpretations.

The way that the visual system addresses this overwhelming expansion of possibilities into the third dimension is to essentially construct, or reify, every possible spatial interpretation simultaneously and in parallel, a computational function only possible in a parallel analog wave-based system. Competition between alternative spatial interpretations results eventually to the emergence of the single (or more) interpretation(s) of the stimulus that is (are) consistent with the given stimulus.

The primary function of visual perception