Clifford Algebra, a.k.a. Geometric Algebra, is a most extraordinary synergistic confluence of a diverse range of specialized mathematical fields, each with its own methods and formalisms, all of which find a single unified formalism under Clifford Algebra. It is a unifying language for mathematics, and a revealing language for physics.
Unlike the standard vector analysis whose primitives are scalars and vectors for representing points and lines, Clifford Algebra has additional spatial primitives for representing plane and volume segments in two and three dimensions, and it can be extended to any number of higher dimensions by the same basic scheme, and they do, with remarkably useful properties.
Adding one extra dimension to a total of 4 produces a projective geometry, a concept not exclusive to Clifford Algebra, but very simply expressed in it, with some remarkable invariance properties.
Adding two additional dimensions to a total of 5, enables a conformal geometry with even more extraordinary invariances which are reminiscent of certain properties of perception.
The truth, or validity of Clifford Algebra is confirmed by Occam’s Razor, it provides a simpler model of mathematical objects than does vector algebra, extending naturally from one to two, to three, and higher dimensions all under the same formalism, with a notational economy that simplifies many mathematical expressions.
For example Clifford Algebra reduces Maxwell’s equations of electromagnetism to a SINGLE EQUATION, the rest is implicit in the math!
Another feature of Clifford Algebra is that it uses a coordinate-free representation. Instead of defining motion with respect to an external coordinate system, motion is described with respect to a coordinate frame defined on the object in question, which greatly simplifies many models. Clifford Algebra reveals, for example, that the apparent chirality in electromagnetism, i.e. the right-hand rule for electric generators, and the left-hand rule for electric motors, turns out to be actually an artifact of the math used to describe the world, not a property of the world itself. It turns out that electromagnetism has no chirality, as revealed by Clifford Algebra.
Clifford Algebra fixes many of the problems inherent in linear algebra, from the arbitrary distinction between row-vectors and column-vectors, the complex process of matrix multiplication, the arbitrary arrangement of terms in the matrix, exemplified most clearly by the complexity of the formula for the determinant of a matrix, to determine whether the matrix is invertible. In Clifford Algebra the determinant is the three-dimensional volume of the parallelopiped spanned by the three row vectors of the matrix, and it becomes intuitively obvious that the volume goes to zero when the three vectors are parallel, or when they are all in the same plane. Furthermore, the whole concept of inversion becomes an explicit spatial inversion, a literal turning inside-out of a spatial structure.
Clifford Algebra provides a more intuitive model for subatomic particles that are often modeled with the Pauli matrix, by way of a spatial model that resembles the particle that it models.
And the way that Clifford Algebra achieves this extraordinary Grand Unification of mathematics is by expressing algebraic concepts in the form of spatial operations on spatial structures. Clifford Algebra, a.k.a. Geometric Algebra, is simultaneously a geometrification of algebra, and also an algebrification of geometry. We are accustomed to viewing algebra as a manipulation of abstract symbols back and forth across the equals sign. But do you remember when in geometry, you learned about a transversal crossing a pair of parallel lines, and which angles were similar and which were complementary? Your teacher never had to prove these truths, they merely had to be pointed out, they were self-evident by inspection. Clifford Algebra does that for algebraic manipulations, which become natural and intuitive spatial operations on spatial structures.
Geometry is more primal and explicit than algebra. In Clifford’s own words,
“geometry is the gate of science, and the gate is so low and small that one can only enter it as a child.”
Clifford algebra invites us to stoop low enough to re-examine some of the most basic mathematical concepts that we first learned as children, and to see new spatial and geometrical relations in them.
Why So Obscure?
So if Clifford Algebra is so great, how come you have never heard of it before? In the first place Clifford died at an early age in an era where there were several competing algebras being developed, and Clifford Algebra was eclipsed by Gibb’s Vectors that we all learned in school.
Clifford Algebra was briefly rediscovered by Dirac as a superior expression of his theory of the electron, although the wider significance was not recognized. It was rediscovered again in the 1980’s by David Hestenes who recognized its general applicability and significance, and David has made a careeor of promoting “Geometric Algebra”, a more modern update to the original Clifford Algebra. David Hestenes prefers the term “Geometric Algebra”, which was actually Clifford’s own choice, because “Clifford Algebra” sound like “just another algebra” rather than what it really is, which is a discovery of the fundamental geometrical roots of all of algebra. Besides, Hestenes credits Hermann Grassmann at least equal to Clifford in the development of Geometric Algebra. I use the term “Clifford Algebra” for historical context and honoring a quirky dude, and “Geometric Algebra” when focusing on the modern reformulations and extensions many of which are due to David Hestenes.
My own interest in Clifford Algebra stems from my own conviction that mathematics is not a human invention, but more of a discovery of the foundational principles of thought. Mathematics is an artifact of the human mind and how it represents spatial reality. The properties of mathematics are direct evidence for the principles of operation of the human mind.
And since Clifford Algebra provides such a clear view into the fundamental nature of math, I believe Clifford Algebra to be the Rosetta Stone that reveals the basic computational and representational principles of spatial perception and algebraic cognition.
In fact the many regularities found in mathematics, from the periodicity of the number line, the alternation of even and odd, its mirror symmetry across the origin, and the polarity reversals of negation and inversion, all suggest a phasic / cyclic system of representation not unlike the trace on an oscilloscope in an analog oscillatory circuit, which in turn suggest a wave based representation in the brain underlying both spatial perception and mathematical thought.
Historical Summary
The history of algebra has been a history of the incremental discovery of an apparently pre-existing structure. The natural numbers were discovered independently by all cultures, suggesting that the concept of number is intuitive, or innate. The concepts of zero and the negative numbers seem to follow naturally, as if of necessity, and they too were “rediscovered” independently by different cultures over time.
The closure of circular negation was the first hint of an irregularity.
A problem arose when the solution to certain algebraic equations came out to be equal to the square root of minus one, something that was a mathematical impossibility! Rafael Bombelli, and René Descartes (who coined the term “imaginary” numbers) proposed to name this impossible number i, but that besides the fact that it squares to negative one, in every other way it was a regular number. So for example 1 times i = i. i times i (by definition) = -1. -1 times i must equal -i. And -i times i = -(-1) which brings us back to 1.
 Repeated multiplication by i goes round and round in circles, making periodic excursions into an orthogonal dimension and back again. If you plot the imaginary dimension as a regular spatial dimension, this suggests that multiplication by i corresponds to a 90 degree rotation. This is an example of mathematical closure, a concept we will see again and again in Clifford Algebra.
Repeated multiplication by i goes round and round in circles, making periodic excursions into an orthogonal dimension and back again. If you plot the imaginary dimension as a regular spatial dimension, this suggests that multiplication by i corresponds to a 90 degree rotation. This is an example of mathematical closure, a concept we will see again and again in Clifford Algebra.
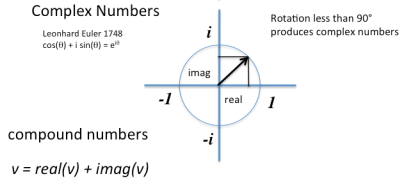
Later it was proposed that you could rotate by less than 90 degrees, which produces a compound number composed of real and imaginary components.
But the real and imaginary dimensions operate by different rules. Multiplication of real numbers scales their magnitudes in or out from the origin. But multiplication of the imaginary component performs a rotation, it is a multiplication that goes round and round instead of in and out.
I don’t know if anyone ever pointed it out to you, but this is VERY STRANGE!
 Josiah Willard Gibbs
Josiah Willard Gibbs
About the same time in the late nineteenth century, Josiah Willard Gibbs was playing around with a different kind of compound number, pairs or triplets of (x,y) or (x,y,z) which can be represented as “directed line segments”, or vectors. The remarkable thing was that you could add or subtract these compound numbers in a manner that made a kind of intuitive spatial sense. The question arose: What happens if you multiply and divide them? Gibbs proposed two kinds of multiplication, the dot product and the cross product, as we all learned in school.
Oliver Heaviside used Gibbs vectors to reformulate Maxwell’s equations of electromagnetism, which did much to cement Gibbs’ vectors position as the dominant paradigm of vector manipulation. Nevertheless, Tait commented that Gibbs’ vectors were “a sort of hermaphrodite monster, compounded of the notations of Hamilton and Grassman”
The dot product was a good idea, and has been incorporated into Clifford Algebra. But it turns out in retrospect that the cross product was a big mistake! In the first place it is only really defined for three dimensions, it does not generalize to two-dimensional vectors without popping out of the page into the third dimension, and in four dimensions the concept is practically meaningless because there are so many orthogonal directions. Furthermore, Gibbs’ vectors can only express scalars and vectors, the only way it could represent a plane is by its surface normal, which is a vector.
Also the cross product can only rotate by 90 degrees, it cannot rotate through intermediate angles as do complex numbers.
 Finally Gibbs’ algebra has a parity problem, the cross product is not preserved under reflection, and thus it introduces a chirality to its model of reality even where there is no chirality in the entity being modeled.
Finally Gibbs’ algebra has a parity problem, the cross product is not preserved under reflection, and thus it introduces a chirality to its model of reality even where there is no chirality in the entity being modeled.
William Rowan Hamilton
In the meantime over in another branch of mathematics, William Hamilton was trying to extend complex numbers, with their elegant rotational multiplication, into three dimensions by proposing three orthogonal imaginary dimensions, i, j,k, each of which behaves like the imaginary dimension i, and they interact with the peculiar circular rule that i x j = k, j x k = i, and k x i = j. Here again we see another example of mathematical closure, a curious property which turns out to be very significant.
But Hamilton ran into a problem defining division for these imaginary vectors because the quotient was not unique. Imaginary vectors A and B, each composed of (i,j,k) components, multiply meaningfully as in A x B = C, but the inverse, C / B does not produce a single unique value but a whole range of possible values. This algebra lacked closure, it only computes one way, you cannot calculate backwards, as in moving terms back and forth across the equals sign.
After many years of frustration, in a flash of intuition (immortalized by a plaque on the Broom Bridge in Dublin where the intuition first struck him) Hamilton realized that he needed one more scalar value to provide a scale for his complex vectors, so he defined a compound number of the form v = a + bi + cj + dk, which could be both multiplied and divided, and the quaternion was born!
All this occurred in the era when the theory of relativity was first emerging, and 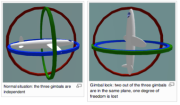 Hamilton incorporated a relativistic concept in his quaternions by expressing rotations not with reference to a global x,y,z coordinate frame, but relative to the current orientation. For example if the orientation of an aircraft in flight is expressed in “Euler angles” as a triplet of roll, pitch, and yaw angles in absolute coordinates, there is a problem known as “gimbal lock” when the aircraft is heading either straight up, or straight down, where it has no defined yaw angle, or heading. Instead, quaternions employ a coordinate system that rotates with the aircraft, as perceived by the pilot in the aircraft, where concepts of “pull up”, “roll left”, and “yaw right” are meaningful whatever the current orientation of the aircraft.
Hamilton incorporated a relativistic concept in his quaternions by expressing rotations not with reference to a global x,y,z coordinate frame, but relative to the current orientation. For example if the orientation of an aircraft in flight is expressed in “Euler angles” as a triplet of roll, pitch, and yaw angles in absolute coordinates, there is a problem known as “gimbal lock” when the aircraft is heading either straight up, or straight down, where it has no defined yaw angle, or heading. Instead, quaternions employ a coordinate system that rotates with the aircraft, as perceived by the pilot in the aircraft, where concepts of “pull up”, “roll left”, and “yaw right” are meaningful whatever the current orientation of the aircraft.
Hamilton introduced another innovative departure from conventional mathematics by proposing a  multiplication which was not commutative, i.e. that a x b is not equal to b x a, but neither are they unrelated, but in fact a x b = -(b x a), where negation corresponds to a reversal in the direction of rotation, just as negation of a real vector reverses its orientation. These intriguing concepts were incorporated into Clifford Algebra.
multiplication which was not commutative, i.e. that a x b is not equal to b x a, but neither are they unrelated, but in fact a x b = -(b x a), where negation corresponds to a reversal in the direction of rotation, just as negation of a real vector reverses its orientation. These intriguing concepts were incorporated into Clifford Algebra.
Closure
Now a word on the concept of closure, which will turn out to be significant throughout this presentation. In algebra closure refers to operations on an algebra that remain within the algebra. For example the natural numbers are closed under addition because the sum of any two natural numbers is also a natural number, but they are not closed under subtraction, because if you subtract enough you can fall right off the end of the natural number scale.
Likewise, the integers are closed under addition, subtraction, and multiplication, but they are not closed under division because certain quotients fall between the cracks of the integers. But that is not the only kind of closure in math.
0 1 2 3 4 5 6 7 8 9
There is closure in our numeral system, where when we run out of digits, we just put a zero and carry to the next column.
There is closure in an odometer where each wheel flips from 9 to 0, and the whole register flips from 99999 +1 to 00000.
There is closure in digital registers that also flip from FFFF +1 to 0000.
It’s a computational principle that prevents the calculation from “running off the edge of the page”, or the register, allowing infinite calculation within a finite representation.
And there is closure in a multiplication that goes round and round instead of in and out. It defines a continuous space like a section of the x axis, but it is a closed dimension, that is finite, but boundless. This will turn out to be very significant.
Hermann Günther Grassmann
 Meantime Hermann Grassmann, the inventor of linear algebra, proposed an alternative to Gibbs’ flawed cross product, in the form of the exterior product, or wedge product, whereby the wedge product of two vectors defines a patch of surface whose area is equal to the product of the two vectors, as if one vector was “swept” along the other (or the other “swept” along the first), and that surface is within the plane that contains both of the original vectors. Just as a vector has magnitude and orientation, but it has no defined location because it is always at the “origin”, in the same way, the bivector, or wedge product of two vectors has an orientation and an area, but it has no location, and neither does it have a shape. It is an oriented area.
Meantime Hermann Grassmann, the inventor of linear algebra, proposed an alternative to Gibbs’ flawed cross product, in the form of the exterior product, or wedge product, whereby the wedge product of two vectors defines a patch of surface whose area is equal to the product of the two vectors, as if one vector was “swept” along the other (or the other “swept” along the first), and that surface is within the plane that contains both of the original vectors. Just as a vector has magnitude and orientation, but it has no defined location because it is always at the “origin”, in the same way, the bivector, or wedge product of two vectors has an orientation and an area, but it has no location, and neither does it have a shape. It is an oriented area.
These bivectors can be added and subtracted just like regular vectors, and if a bivector is multiplied  by a vector, its surface is “swept” along that vector in the same manner to define the volume spanned by the three component vectors, an entity known as a trivector. In other words, this is an algebra that generalizes to higher dimensions by the same exact principles that apply at the lower dimensions, and this provides an algebraic entity for scalars, vectors, bivectors, trivectors, and there is no limit to the number of dimensions it can be extended to.
by a vector, its surface is “swept” along that vector in the same manner to define the volume spanned by the three component vectors, an entity known as a trivector. In other words, this is an algebra that generalizes to higher dimensions by the same exact principles that apply at the lower dimensions, and this provides an algebraic entity for scalars, vectors, bivectors, trivectors, and there is no limit to the number of dimensions it can be extended to.
Like Hamilton’s quaternions, Grassman’s wedge product is anti-commutative, whereby a^b = -(b^ a). And it also incorporated a kind of closure whereby (in three dimensions) a^b^c makes a trivector, but a^b^c^d collapses back down to a scalar so as to prevent runaway expansion into ever higher dimensions.
a). And it also incorporated a kind of closure whereby (in three dimensions) a^b^c makes a trivector, but a^b^c^d collapses back down to a scalar so as to prevent runaway expansion into ever higher dimensions.
William Kingdon Clifford
William Kingdon Clifford was the man who took all the best ideas from previous work to achieve a single consistent formalism that generalizes to arbitrary numbers of dimensions. Clifford defined a hierarchy of compound number knows as “clifs”, or “multivectors”, that range from zero dimensions (scalar) to one dimension (vector) to two dimensions (bivector), to three (trivector), and on upward as far as you care to go. In Clifford Algebra dimensions are referred to as “grades”, so a scalar is grade zero, a vector is grade 1, etc.
In order to attain the kind of closure seen in quaternions, you have to decide from the outset how many dimensions you want to use for your problem, so for example two-dimensional Clifford algebra, or Cl2 wraps around at two dimensions so as not to protrude out of the plane into the third, whereas Cl3 has closure in three dimensions, so as not to protrude into the fourth.
Just as a real number can be considered as a complex number with zero imaginary component, a clif  can be considered to be composed of higher order clifs up to the grade of the algebra you choose, even if many of them happen to have zero coefficient for any particular problem. Clifford Algebra of zero dimensions, Cl0, is just regular scalar algebra. Clifford Algebra of one dimension, Cl1, is composed of a scalar and a vector. Cl2 is composed of a scalar, two vectors, and a bivector. Cl3 is composed of a scalar, three vectors, three bivectors, and a trivector, and that same scheme extends upward to higher dimensions by the same principle.
can be considered to be composed of higher order clifs up to the grade of the algebra you choose, even if many of them happen to have zero coefficient for any particular problem. Clifford Algebra of zero dimensions, Cl0, is just regular scalar algebra. Clifford Algebra of one dimension, Cl1, is composed of a scalar and a vector. Cl2 is composed of a scalar, two vectors, and a bivector. Cl3 is composed of a scalar, three vectors, three bivectors, and a trivector, and that same scheme extends upward to higher dimensions by the same principle.
Here we see the hierarchy of Clifford Algebras each with its own characteristic pattern of components, that appear in numbers corresponding to Pascal’s triangle. Two-dimensional clifs, Cl2 (the even sub-algebra) are mathematically isomorphic to complex numbers. Three-dimensional clifs, Cl3 are isomorphic to Pauli matrices used to model subatomic particles. Cl4 is isomorphic to Dirac matrices that model relativistic subatomic particles.
Pauli matrices used to model subatomic particles. Cl4 is isomorphic to Dirac matrices that model relativistic subatomic particles.
Lets take a closer look at Cl3, Clifford Algebra in three dimensions. There is a scalar, e, then three orthogonal basis vectors e1, e2, e3, then three bivectors obtained by pairwise multiplication of the basis vectors, and finally a trivector defined by the wedge product of all three basis vectors. Each bivector has a kind of twist that represents a rotation by 90 degrees, for example bivector e1^e2 represents the right-angled turn from the direction e1 to e2, while its negation, -(e1^e2) rotates by the same angle but in the opposite direction.
Multiplication of all three basis vectors (e1^e2^e3) produces a three-dimensional volume segment or trivector, with unit cubed volume. This trivector has some peculiar properties that represent the scale of the whole space, it is often called the pseudoscalar of the space, I, it performs the function of the imaginary number i, but extended into three dimensions. Multiplication by the trivector represents a 90 degree turn in all three dimensions. Therefore two such 90 degree turns in each of the three dimensions results in a total reversal of direction, which is equivalent to a simple negation, and thus I**2 = -1. Clifford Algebra eliminates the mystery of the concept of the imaginary number, which becomes a simple rotation by 90 degrees.
For all the variety of different clifs of their various grades, there are basically two ways that clifs can interact, one is addition/subtraction (add-traction?) and the other is multiplication/division (multipli-vision?). Addition represents a kind of summation of independent or successive processes, whereas multiplication represents a simultaneous modulation of one clif by another; if either clif is negative the product is negative, but if both are negative the product is positive again, another manifestation of closure. In fact analog modulation as in AM radio, or linear gain in amplification, is defined exactly as analog multiplication.
These two very basic and primal operations can be applied between clifs of any grade, and they can be applied across different grades, and in every case they produce results that seem intuitively consistent and reasonable as one might expect. Addition of scalars and vectors produces a compound scalar and vector product. Addition of vectors proceeds logically as in Gibbs’ vectors. Bivectors add to other bivectors to produce a sum bivector.
A scalar times a vector scales the vector in length, and reverses its direction if negative. A vector times a vector makes a bivector with a twist that turns from the direction of one to that of the other. A scalar times a bivector scales its area. A vector times a bivector, or the product of three vectors produces a trivector. A vector times a trivector does not expand to a quadrivector, but rather it collapses back down to a scalar, thus maintaining closure in three dimensions.
There is an interesting interaction that occurs across grades seen for example when a scalar, a non-spatial entity, multiplies a vector which has linear extent, it changes the spatial length by the magnitude determined by the scalar value. Likewise, taking the magnitude of a vector v as in ||v|| summarizes the spatial extent of that spatial vector with a non-spatial scalar magnitude. A bivector B can also be reduced to a scalar magnitude by taking its magnitude ||B||, which provides an abstract measure of the magnitude of the bivector which is proportional to its area. These are manifestations of inter-grade communication, whereby the scalar value can be seen as the most abstract representation, reducing clifs to a single scalar value that records their magnitude, and thus scalar algebra can be seen as an abstraction of the principles of vector algebra, preserving the corresponding magnitudes but discarding spatial extent.
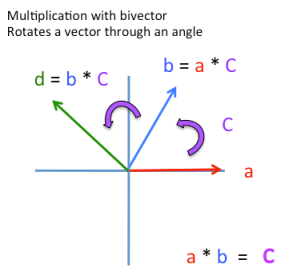
Lets take a closer look at the product of two vectors. If the two vectors are parallel, the product collapses to a scalar, yet another manifestation of closure. A vector times itself collapses to a scalar value one, meaning the vector is a perfect match to itself. If the vectors are pointing in different directions, the product includes a bivector with a twist proportional to the area spanned by the two vectors.
 We can see the effects of the twist by multiplying a different vector by the bivector, which rotates the vector through the same angle as that between the original vectors. Vector a times bivector c (= a x b) rotates a through the angle from a to b, which leaves it equal to b. Vector b times bivector c produces d, rotated from b through the same angle as that between a and b. As with quaternions,
We can see the effects of the twist by multiplying a different vector by the bivector, which rotates the vector through the same angle as that between the original vectors. Vector a times bivector c (= a x b) rotates a through the angle from a to b, which leaves it equal to b. Vector b times bivector c produces d, rotated from b through the same angle as that between a and b. As with quaternions,
Since Clifford multiplication is anti-commutative, it is important to distinguish a*b from b*a, depending on which is the pre-multiplier and which the post-multiplier. For example a*b is a rotation from a to b, when applied to a, as in a*(a*b) it rotates a into b, or b = a*(a*b). But the term can be grouped differently by moving the parentheses, i.e. (a*a)*b. Since a*a = 1, (a*a)*b = b, which produces the same result, so everything works out right in the end.
The Geometric Product
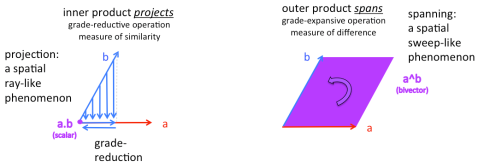
As with Gibbs’ vectors with its distinction between the dot and cross products, Clifford multiplication, known as the geometric product, is actually a compound multiplication composed of the sum of a dot product and a wedge product. Like Gibbs’ vectors, this product captures two aspects of multiplication. The dot product is a measure of similarity between two vectors, and is a scalar quantity, whereas the wedge product is a measure of difference, or what you’d have to do to one to transform it into the other. These are complementary operations, each one capturing what the other misses. Significantly, both are spatial projective operations, one is grade-reducing projection, the other is grade-expanding sweep. The inner product projects one vector onto the other like casting a shadow, although the shadow is then projected again to a scalar magnitude. The outer product spans the space between the vectors, a spatial sweep-like operation that is grade-increasing.
These two operations are not just complementary by design, but by definition. The dot product is computed as the (average of the) product, a*b, added to its reverse b*a. Adding a product to its reverse cancels out any component that is asymmetrical, i.e. the clockwise twist cancels its counter-clockwise reverse, leaving only the symmetrical component, which is the dot product, or what the two vectors share in common. It is a little peculiar to call this operation a “multiplication”, because multiplication is generally thought of as producing a multiplicity of its multiplicands; it is generally an expansive operation (unless the multiplicands are less than one), whereas the dot product is more like a collapse to lower grade, more akin to what we think of as division.

The wedge product is defined as the (average of the) difference between the product and its reverse, an operation that eliminates the symmetrical component, but the reversal of the reverse by negation makes them both rotate in the same direction, whose average preserves only the asymmetrical component, that represents the difference between the vectors, or how one is twisted from the other. The dot and wedge products are therefore like symmetry filters that filter the symmetrical and asymmetrical components of their multiplicands, respectively.
 A (scalar ^ a vector) makes a vector. A (vector ^ a vector) makes a bivector. A (bivector ^ a vector) makes a trivector. The wedge product is a grade-increasing operation. A trivector dot a vector collapses the dotted dimension. Trivector (P^Q^R) . R collapses the R dimension to make bivector P^Q. Bivector (P^Q) . Q collapses to P. Vector P dot P collapses to 1. The dot product therefore seems more akin to division than to multiplication.
A (scalar ^ a vector) makes a vector. A (vector ^ a vector) makes a bivector. A (bivector ^ a vector) makes a trivector. The wedge product is a grade-increasing operation. A trivector dot a vector collapses the dotted dimension. Trivector (P^Q^R) . R collapses the R dimension to make bivector P^Q. Bivector (P^Q) . Q collapses to P. Vector P dot P collapses to 1. The dot product therefore seems more akin to division than to multiplication.
It is interesting to note that a scalar * scalar * scalar * scalar is still a scalar! You need to have at least one spatial dimension to start expanding in grade. The basis vectors e1 e2 e3 can be thought of as pre-existing “generators” capable of generating a vector as soon as they are supplied with a non-zero coefficient.
Here is an animation of the product of the two red vectors as one rotates around the other, showing the complementarity of the dot and wedge products. (The dot product is depicted here as a vertical vector, to show its magnitude, although it is actually supposed to be a scalar quantity) Note the several polarity reversals of both the dot and wedge products as as the vectors go around, along with a reversal in the rotational orientation, or “twist” of the bivector.
Clifford Vectors Analog Electronics Analogy
This series of phase reversals, and the concept of a generator, is highly suggestive of a cyclic phasic representation not unlike the trace on an oscilloscope, as demonstrated in the above op-amp circuit. A sawtooth waveform generator at the upper-left generates the sawtooth wave plotted on the lower left, which is split into x and y streams each of which can be modulated by the potentiometers toward the right to produce X and Y traces whose amplitude can be modulated (and reversed) with the X and Y sliders to the right, plotted at the lower center of the screen. The X and Y signals are then plotted against each other at the lower right, showing a “flying spot” starting at the origin and flying cyclically toward the upper-right, tracing out the vector represented by the oscillations in the system. If you reverse the X slider the vector rotates into the second quadrant. If you then reverse the Y slider the vector rotates into the third quadrant, if you reverse the X slider back to positive the vector rotates into the fourth quadrant, and if you bring Y back to positive the vector returns to the first quadrant. The sawtooth waves that control the “flying spot” that traces out the vector correspond to the basis vectors e1 and e2, which are constantly cycling, but only produce a trace when their coefficient is non-zero.
The basic principles behind Clifford Algebra appear rather simple, which makes it all the more wonderous what complex computations they can achieve.
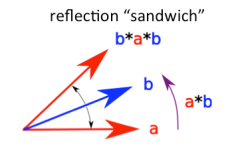
Clifford Algebra has been characterized as a “reflection algebra” because its most primal operation, vector multiplication, seems to mimic a simple reflection. If red vector c = b*a*b is the product of b times (a*b), it is a reflection of a through b, because the angle from c to b is the same as the angle from b to a. (We are dealing here with unit vectors so as to avoid any additional scaling, resulting in pure rotation)
This Clifford Vector Multiplication Animation shows how the reflection of a in b occurs like a reflection in a plane surface normal to vector b.
The rich and powerful operation of that rotational Clifford multiplication can be reduced to a simple reflection!
This rotational multiplication by reflection is reminiscent of a phenomenon in nonlinear optics when two laser beams cross in space, as shown for beams B1 and B2 above. An interference pattern appears through the zone of their intersection due to constructive and destructive interference. If modeled in a Reciprocal Lattice representation where each beam is represented by a vector, as shown by K1 and K2 in C above, the emerging interference pattern can itself be described as the difference vector K2 – K1 that closes the wave vector diagram.
If the crossing occurs in empty space it has no effect on anything else. However if the crossing takes place in the transparent volume of a nonlinear optical materal (and most any glass goes nonlinear with sufficient amplitude) the interference pattern warps the glass in the shape of the pattern, by the optical Kerr effect, which defines parallel planes of alternating refractive index in the glass.
This reified interference pattern in turn is able to deflect, or reflect a third beam, B3 above, producing a fourth reflected beam B4 whose direction and magnitude can also be computed as the vector that closes the wave vector diagram in the reciprocal lattice representation in B above, i.e. such that K1+K2+K3+K4 = 0. This is the principle behind phase conjugation, a mechanism by which the angle between two vectors controls the reflection of a third, reminiscent of the bivector and its effect on vectors that are multiplied with it.
Maxwell’s Equations in Clifford Algebra
The power of the geometric product is demonstrated most dramatically in the example of Maxwell’s four Equations of Electromagnetism. These describe the curl of electric and magnetic fields using cross-product terms, and the divergence of the electric and magnetic fields using dot product terms.
The magnetic field must be described by a “pseudo-vector” field because unlike a plain vector, as with the electric field, the magnetic field cannot survive an “improper rotation” i.e. a reflection without requiring an additional change of sign. (The mirror image of your right hand demonstrating the right-hand rule is your left hand, but that demonstrates a left-hand rule!)
In Clifford Algebra these four equations reduce to a single equation, the rest is implicit in the math! The magnetic field is described by a bivector, which has the sign-flipping automatically built-in. The geometric product product automatically multiplies the wedge product terms for the curl, and the dot product terms for divergence, all in a single equation.
Algebraic / Spatial Concepts
There are a number of algebraic concepts, some of which are familiar in scalar algebra, that are revealed by Clifford Algebra to be actually algebraic / spatial concepts. For example the reflection of a vector about the origin is equivalent to negation. Reflection is negation! Clifford Algebra is a reflection algebra. Rotation by 180 degrees is also a negation! Rotation by 90 degrees is equivalent to multiplication by i, the square root of minus one, because two of those multiplications reverse the direction which is also negation. This removes the mystery behind that peculiar notion of the square root of minus one, and reveals it to be a simple rotation. Furthermore, negation is also rotational reversal, thus drawing an equivalence between the open translational dimensions and the closed circular dimensions. This is very strange! Its profound significance will be discussed below.
This is simultaneously an algebrification of geometry, and the geometrification of algebra, it suggest a fundamentally spatial computational mechanism behind the principles of algebra. The similarity between numbers arrayed along the number line, and the lengths of corresponding vectors from the origin, is no mere coincidence, it reveals spatial vectors as the true basis underlying even scalar algebra.
It is a peculiar characteristic of Clifford Algebra that angles are not represented directly as angles, expressed in degrees or radians, but rather, angles are expressed by their X and Y components, a rectilinear coordinate system for expressing angles. This is significant because it makes a connection between the egocentric “dartboard” polar coordinate system where the origin is a special unique place, and the allocentric “city-block” Cartesian coordinate system in which every point is identical, and the origin is no longer special. Clifford algebra expresses one in terms of the other, thus mapping them to each other.
Another curious algebraic / spatial concept is the Dual, indicated by a superscript* asterisk. Every Clifford Algebra entity has its “orthogonal complement”, like the particle and its antiparticle, or the yin and its yang. For example the dual of a vector is a bivector, the wedge product of a pair of vectors that are orthogonal to it, and the dual of the bivector is its normal vector. The area of the bivector that is the dual of a vector is proportional to the magnitude of the vector.
The dual of a scalar, which has no spatial extent, is the pseudoscalar, which has all the spatial extent, and the dual of the pseudoscalar is a scalar.
The dual of a clif is easy to calculate, you just divide by the pseudoscalar, and this is a consequence of closure, because a vector times itself collapses to a scalar, so multiplying by the pseudoscalar collapses all vectors that are non-zero, leaving only those that were zero to begin with. It flips the whole pattern into its opposite, and the opposite of the opposite is back again to the apposite, the thing you began with in the first place.
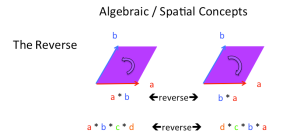
Another algebraic / spatial concept is the reverse. For example the reverse of a*b is b*a. The reverse of a*b*c*d is d*c*b*a. Its like multiplying yourself back out again in the reverse sequence than the way you got in. We have already seen the utility of the reverse in defining the dot product and the wedge product by symmetry and anti-symmetry respectively.
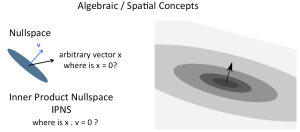
Another interesting concept is the Nullspace, defined for a Clif as the set of all vectors that evaluate to zero for some function. For example the Inner Product Nullspace (IPNS) of a vector v is the set of all vectors whose dot product with v = 0, which consists of the plane that is orthogonal to v. This is in contrast to the dual of that same vector, which is a bivector normal to the vector, i.e. within the plane of the IPNS, but with an area proportional to the length of the vector, whereas the IPNS of a vector is a plane that extends to infinity. This is a generalization of the outer product to infinity. (Note that the NULL in the nullspace is a negation, thus the Inner Product NullSpace resembles an OUTER product, while the Outer Product NullSpace resembles an INNER product)
The Outer Product Nullspace (OPNS) of a vector is the set of vectors whose outer product is zero, i.e. the infinite line within which the finite vector is embedded. Again, this contrasts with the dual of a bivector which is a vector whose length is proportional to the area, whereas the OPNS of a bivector is a line that stretches to infinity in opposite directions.
These are all examples of the principle of reification, extrapolating a given local pattern outward to infinity by the same rules. A vector expands to an infinite line, a bivector surface segment expands to an infinite plane. It is easy enough to comprehend and to describe this kind of reification, but very hard to implement in any kind of finite mechanism, except by a parallel analog spatial principle like an optical mirror system.
Projections are so fundamental to Clifford Algebra that they can be expressed very simply using dot and wedge products.
For example a vector a can be decomposed into parallel and perpendicular components to a plane defined by bivector B, where the parallel component, “a par B” = a.B/B, whereas the perpendicular component “a perp B” = a^B/B. David Hestenes calls this powerful pair of complementary concepts “projection” and “rejection”.
We have seen how reflections can be performed by multiplication. Reflections can also be computed from simple projections. For example the reflection of vector a in bivector U above can be calculated as the component parallel to the plane minus the component perpendicular to it, i.e. “par – perp”.
Rotation by reflection produces a mirror-image reversal in the reflection, as does a normal mirror. This is not readily apparent in the case of vectors due to their one-dimensional symmetry, but is of significance for higher order clifs.
A more general concept of rotation is derived by two reflections through two vectors, which flips the reflection back again, resulting in a rotation without flipping. For example vector “bab” which is (b*a*b) is a reflection of vector a through b, and similarly, the reflection of bab on vector c is computed as c*bab*c, a double reflection “sandwich”
This concept extends naturally into 3-D. For example vector a is reflected through n by the rotation n*a*n, (start with n, then rotate through the angle from a to n) and then that vector “nan” is reflected through another vector m, resulting in a final product of m*nan*m, or m*n*a*n*m.
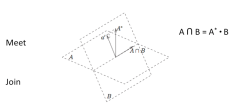
Another algebraic / spatial concept is the concept of the “meet” and the “join” between two Clifs corresponds to the Intersection and Union of the component entities. These too have simple formulas in Clifford Algebra.
The Inverse Function
Now we come to the concept of inversion, 1/x, a concept you learned so long ago that you probably can’t even remember learning it, but in all the time since then, nobody ever pointed out to you that it is a conceptual impossibility! Supposedly for every value x that can range from one to INFINITY, there is a reciprocal value 1/x that is confined to the interval between zero and one. That suggests a one-to-one mapping from an infinite range to a finite range between zero and unity!
This is demonstrated here by plotting in red the reciprocal function between zero and one, i.e. the number whose inverse maps to it. For example ½ maps to 2, 1/3 maps to 3, ¼ maps to 4, and so forth, showing how the inverse function (the red plot line between zero and one) is like a conformal reflection of the number line (the black line plotted from one towards infinity) reflected through the unit boundary although squashed by a conformal mapping.
Its as if you took the number line from one to infinity, made a mirror-image reflection of it, take the reciprocal of that, Then we effectively put a bracket BEYOND INFINITY (the arrow coming in from the left) and squash the reflection back down to a finite range so that the entire reflection is squashed into the unit interval. This is a completely impossible operation because it pretends that it is possible to place a bracket beyond infinity and to squash infinity back to “finity”, a finite range. And on our familiar number line the same operation is done in the negative direction too. This creates a double mirror image of the whole number line from negative to positive infinity excluding the unit radius, all packed within the finite range of the unit radius from -1 to +1. This is an extraordinary paradoxical impossibility, but it is the impossibility that brings closure to multiplication, that offers a reciprocal to multiplication as if every positive and negative number had a reciprocal value that falls between positive and negative unity, and the fact that every number has its reciprocal is what makes it possible to multiply and divide both sides across the equals sign, to calculate forward to compute implications, as well as backward to impute original causes.
This incredible “impossible” reciprocal function was already present in scalar algebra that we learned in grade school. What Clifford Algebra adds to this concept is a circular symmetry, like a set of number lines rotated through all orientations, tracing a unit-radius circle at the center, within which is a conformal reflection of the infinite surrounding space. For every (x,y) point in two-dimensional space that falls on some radial ray from the origin, there is a reciprocal point that falls on the same ray in the same direction from the origin, but with radial distance from the origin that is the reciprocal of the distance to the point, just as occurs on the regular number line itself. If the original point is greater than unity, then its reciprocal is always less than unity, and vice-versa, because by symmetry, the reciprocal of a reciprocal gets back to itself. Clifford Algebra generalizes the algebra on the familiar number line to an algebra that occurs symmetrically at all orientations equally, and thus merges algebra with its parent geometry to define an algebra of space. And this same concept extends naturally into three dimensions and higher, where the central unit-radius sphere, or hyper-sphere, contains within it a reciprocal inverse conformal reflection of the entire space outside the sphere squashed into a finite spherical volume.
Play around with MathForum.org‘s Inversion of A Point Demo and observe that when point x and its inverse point 1/x are close to the circumference of the unit circle, they are mirror-reflections of each other across the unit circle, showing how multiplication is reflection near the unit boundary. When you slide point x off outward towards infinity, its reciprocal point 1/x begins to approach zero, but never gets there unless you could slide x all the way out to infinity! Now if you slide x back from infinity and make it cross the unit circle, it changes place with its reciprocal doppelgänger like Alice changing places with her own reflection in a mirror, and now as x approaches the central origin, its reciprocal shoots off towards infinity. The difference this time is that you can move point x exactly to zero, which means that its reciprocal must have arrived at actual infinity, although no computer display could possibly show it there, we just stop accounting for it when it runs off the edge of our screen.
Alexandre Duret -Stereographic projection
Alexandre Duret’s photo art Stereographic Projection gives an impression of how this idea would look extend into three dimensions, with a spherical boundary at a unit distance from some origin, containing an inverse conformal reflection of the surrounding world. See the tall tower at 2 o’clock, blocking the sun, and its inverse reflection within the unit radius in the 2 o’clock direction, with a peculiar inversion: the tower itself extends outward from the center above its base (“up” is “outward”). In the reflection the tower extends inward from the base toward the center, (i.e. “up” is now “inward”) because in the inverse world, the direction towards the circumference of the circle is proximal, whereas the direction towards the center of the circle is distal, with the bizarre peculiarity that the singular point at the very center of the picture represents infinity in all directions! This is a very strange singular structure to be found at the very core of our number system! It is not there by accident. It provides a lever balance across the unit boundary between a value x and its reciprocal 1/x.
The inverse function embodies an assumption that all of infinity in every direction can be packaged as its reciprocal within a finite unitary range, the finite range from zero to one reflects the entire world from one to infinity. And even more outrageous to common sense, is the fact that although every direction in space points outward towards its own unique infinity in that direction, in the reciprocal reflection they all map to a single central point, which represents not only infinity, but all of the infinities in all directions simultaneously!
In my next post I will show how the impossibility of the inverse function suggests that the number line should not be conceived as infinite, but merely a pseudo-infinity that represents the entire range from one to infinity, all squashed into a finite range, a mirror-image of its conformal reflection, as suggested in non-euclidean geometries.
And of course the same thing would be required in the negative direction. That would render the point-for-point mapping between x and its inverse 1/x no longer an impossible paradox, but now perfectly possible, because it is now a point-for-point mapping from a finite range to another finite range. The existence of the paradox of the inverse function is evidence that our true representation of mathematics in our mind does not use a representation that extends to infinity (how could it?) but it simulates infinity within a finite representation that does not incorporate a paradoxical impossibility.
In fact this much should have been obvious by inspection of our world of perceptual experience, which itself seems to be trapped in some kind of egocentric warp. The sides of a long straight road converge to a point on the horizon before us, and if we turn around, they converge to a point back there too! And yet they appear to be straight and parallel and equidistant throughout their length. This reveals a conformal warp in our very perception of space, such that lines that curve along with the warp are by definition “straight” in that space, and they terminate at (pseudo-) “infinity” at either end. The dome of the sky marks the outer boundary of our perceptual bubble, the maximal extent of our spatial experience, no matter how large a space we are exposed to.
The reason for the warp in our perceptual bubble is clearly to allow a finite spatial representation to depict a practically infinite surrounding space. This is yet another manifestation of closure, with remarkable similarities to the true nature of the number line as revealed by Clifford Algebra.
In my next posting I will show how the similarity with perception does not end there, and that the conformal mapping in Geometric Algebra suggests a similar inversion as a part of perception, except extended out into three dimensions, and the purpose of that inverse representation is the same purpose it serves in mathematics, it reveals certain regularities and symmetries that are not readily apparent in the non-inverse world.
Conclusion
The history of algebra has been the history of an incremental discovery of an evidently pre-existing structure. Clifford Algebra has turned out to be the lynchpin that shows how all the previous discoveries are interrelated within a single self-consistent scheme whose laws operate the same in all directions. It is the very simplicity and generality of Clifford Algebra that confirms its “truth”. But truth to what? What is it that mathematics represents? What must it remain true to? This gets to the question of, as Lakoff and Núñez (2000) called it in the title of their book, “Where Mathematics Comes From“. If algebra is the discovery of a pre-existing structure, then what is that structure and where is it located? Plato and his many modern adherents believe mathematics to be an objective eternal Truth that exists independently of human minds, although it is only accessible through the human mind. It is true that mathematics is not a human invention, but more of a discovery, and thus has objective existence in that sense. But to declare the magnificent edifice of Mathematics to inhabit an orthogonal dimension that is inaccessible to scientific scrutiny, is a hypothesis that cannot in principle be falsified, and thus, it is not a scientific hypothesis but more of a belief, for those who are inclined to believe it. I demand a more scientifically sound falsifiable hypothesis for the ultimate nature of mathematics that gives it objective existence in the universe known to science. I agree with Lakoff and Núñez that mathematics is an artifact of how our mind makes sense of reality, and that therefore mathematics has physical existence or instantiation within the human brain. Our view of the world is not direct, we see the world indirectly, through a representation, or model of the world constructed in our brain, and that model is painted out in the geometric primitives of points and lines and planes, which are the elemental features of perception, and those geometric primitives correspond closely to the algebra which was ultimately derived from them. Since Clifford Algebra offers such a clear view of the essential principles of mathematics, it thereby also offers a clear view of the principles of visual perception and the way we conceptualize shapes in space, revealing algebra to be at the root of it a spatial process of spatial operations that operate on spatial structures. The scalar algebra that we learn first in school is an abstraction of the vector algebra that underlies it.
The periodicity of the number line, the alternation between even and odd, the concepts of negation and inversion, are all strongly suggestive of a phasic cyclic oscillatory phenomenon which must ultimately reside in the brain. The fact that Clifford Algebra reveals all of algebra to be a spatial phenomenon at the root of it, suggests that the computational processes of the human brain are themselves spatial in nature, like the computational operations of nonlinear optics and phase conjugation which they resemble, where spatial waves interact with other waves to produce modulated waves. The fact that Clifford algebra is particularly good at modeling phasic / cyclic phenomena such as the “spin” of elementary particles, all suggests that the human brain operates with a spatial representation based on cyclic oscillations and standing waves in the brain, which just happens to be similar to the cyclic resonances of subatomic particles. The equivalence found in Clifford Algebra between the linear and rotational domains, how negation maps also to rotational reversal, and translation along a linear axis maps to angular rotation about the origin, is surely further evidence for a wave based principle of computation in the brain. Light waves come in the form of transverse waves that oscillate vertically or horizontally, but it also manifests in the form of rotational oscillations whereby the photon spirals either clockwise or counter-clockwise as it travels through space. It is the essential equivalence between linear and rotational oscillations that reflects their equivalence in Clifford Algebra.
The many manifestations of closure seen in different forms throughout algebra suggests a computational principle that makes optimal use of a finite representational resource, like the odometer whose individual dials each form closed loops, as does the odometer as a whole, and thus the mechanism never “runs off the end”, it just wraps around again. This is not a strategy for an accurate representation of an effectively infinite universe, as we discover whenever our odometer “rolls over” to zero, but rather it is a strategy for a wise design of a limited representational resource. It is an artifact of the computational mechanism of our numerical mind with which we represent the world, not a property of the world itself. But there is also a certain invariance to a rotational representation that resolves the problem of the “infinities” found at both ends of every number line. The equivalence between linear and rotational dimensions suggests that our mind never actually uses linear dimensions like the X axis, but approximates them in a circular dimension to avoid the problem of “infinities”.
This entire analysis of Clifford Algebra was based on my own foundational assumption that mathematics is not a human invention, but more of a discovery of the essential principles of computation in the brain. If this hypothesis is correct, then it should be possible to reverse engineer the principles of operation of the brain with guidance from the properties of mathematics as revealed through Clifford Algebra. I propose the next step in investigating the computational principles of perception would be to devise oscillatory circuits such as this Clifford Vectors Analog Electronics Analogy, to see what is possible using waves as a principle of spatial representation and computation. When we discover what kinds of things can be computed using a cyclic / phasic analog system built to emulate Clifford Algebra, only then will we be ready to hypothesize the computational function of the oscillations found in the brain.
This concludes my introduction to Clifford Algebra, but this is by no means the end of the story! This narrative continues with the story of Geometric Algebra, the modern reformulations and some extraordinary extensions to Clifford’s and Grassman’s work, largely due to David Hestenes, that reveal the true potential of Clifford Algebra and its intimate connection with perception. David Hestenes saw fit to rename Clifford Algebra to Geometric Algebra, which it turns out was Clifford’s own choice, because Hestenes wanted to emphasize the fact that Clifford Algebra is not just another algebra, but a radical discovery of the true roots of all algebras, and those roots are geometric in nature.
The story continues with Geometric Algebra: Projective Geometry.
The final chapter is Geometric Algebra: Conformal Geometry.









































































I like your introductory presentation of Clifford Algebra. I am a physicist/electronics engineer and came up with short a course (more like a “Demo”) on the physical applications of Cl3,0(R) on Twitter. Search for both my user name and the hash tag simultaneously: @stanbles #cliffordalgebra
Regards,
Stan
@paganheretic, is there a link to your demo out of twitter in a pdf/doc? i get a bunch of tweets when i perform the search you mentioned.
if you have a document, i’ll be happy to check out.
They all come complete but out of order. I will post a pdf version of it
on my blog web site
Clifford Algebra Course on Twitter
https://drive.google.com/file/d/15fTvrmP-Fht-u5iMMsq-4ie-7yEcgOcA/view?usp=sharing
More articles are on: http://stan-heretic.blogspot.com/
(left upper corner when using desktop view, GKW when using mobile)
Pingback: Welcoming Steven Lehar as a QRI Lineage | Qualia Computing
” A vector times a trivector does not expand to a quadrivector, but rather it collapses back down to a scalar, thus maintaining closure in three dimensions.”
Thanks for this very helpful guide. Yet I’ve been completely stuck on the above sentence. Doesn’t a vector times a trivector (in 3D) produce a bivector, not a scalar? For example, doesn’t e1*(e1*e2*e3) = e2*e3?
cf. page 23 of https://www.ime.unicamp.br/~agacse2018/GA_Lecture1.pdf (“The PseudoScalar in 3d”)…?
I’ve been stuck on this sentence. Doesn’t a vector times a trivector (in 3D) produce a bivector, not a scalar? For example, doesn’t e1*(e1*e2*e3) = e2*e3? cf. page 23 of https://www.ime.unicamp.br/~agacse2018/GA_Lecture1.pdf (“The PseudoScalar in 3d”)…?
(perhaps older comments address this but the page isn’t displaying them to me)
I think you might be right. I’m really a newbie with Clifford Algebra. But yes, it collapses dimensions one by one with each vector.
Re: “Doesn’t a vector times a trivector (in 3D) produce a bivector, not a scalar? For example, doesn’t e1*(e1*e2*e3) = e2*e3?” – Yes it does and the trivector i := (e1*e2*e3) is pseudo-scalar which behaves like imaginary unit. It is commutative with every other vector (it can be easily proven) and i^2 = -1. And of course i*e1=e1*i = e2*e3 is a bivector indeed. The 3-rg grade Clifford Algebra Cl3,0(R) can be “self-complexified” using trivector i as the imaginary number unit. Clifford algebra described by the 8-Dimensional base vector set {1, e1, e2, e3, e1e2, e2e3, e3e1, i} x R is isomorphic with the 4-Dimensional complex Clifford algebra Cl(2)xC (which incidentally, is isomorphic with Dirac’s spinor space), which can be written symbolically as {1, e1, e2, e3} x C (R=Real, C=Complex number field, notice that e3=-i*e1*e2). Clifford Algebra Cl3,0(R) describes the entire physics as we know it.
Yes, makes sense. Thanks for the clarification. I’m kind of a newbie on Clifford Algebra.
Pingback: [ ]More Q&A to The Domain Commander using my EBP
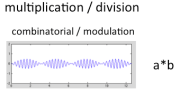
“…two ways that clifs can interact, one is addition/subtraction (add-traction?) and the other is multiplication/division (multipli-vision?). Addition represents a kind of summation of independent or successive processes, whereas multiplication represents a simultaneous modulation of one clif by another.”
You represented these two possible interactions with clipart of what appears to be a transverse wave for addition/subtraction, and a longitudinal wave for multiplication/division.
Did you intend to evoke the idea of wave forms? Perhaps I’m misreading the meaning of the illustrations? Its a very thought provoking idea indeed!
Look at a typical math equation
ax * by / c^2 + dx + ey / 4c …
It is starkly divided into “terms”
(ax * by / c^2) + (dx + ey / 4c) …
Within the terms the variables are fused or melted into each other by multipli-vision. If any variable is zero or infinity the whole term is affected.
Between the “terms” are the add-traction elements joined with + & -. These have an additive or subtractive unaffected by any other terms going to zero, each term is evaluated independently before they are added or subtracted from each other.
I picked a wave as an example because it has the same effect. When you multiply within the terms the whole term is modulated by each of its multiplicative components, but the terms themselves operate independently of the others.
Yes I have waves in my mind because waves exhibit that same distinction between multipli-vision and add-traction.
Thanks for your recognition that this is thought provoking. I like to do math in pictures to express the concept in intuitive picture form. I propose that math is computed in the brain by waves of activation in the brain.